In a 2×2 MIMO channel, probable usage of the available 2 transmit antennas can be as follows:
1. Consider that we have a transmission sequence, for example x1,x2,x3,.....xn
2. In normal transmission, we will be sending x1 in the first time slot, x2 in the second time slot, x3 and so on.
3. However, as we now have 2 transmit antennas, we may group the symbols into groups of two. In the first time slot, send  and
and  from the first and second antenna. In second time slot, send
from the first and second antenna. In second time slot, send  and
and  from the first and second antenna, send
from the first and second antenna, send  and
and  in the third time slot and so on.
in the third time slot and so on.
4. Notice that as we are grouping two symbols and sending them in one time slot, we need only n/2 time slots to complete the transmission – data rate is doubled !
5. This forms the simple explanation of a probable MIMO transmission scheme with 2 transmit antennas and 2 receive antennas.
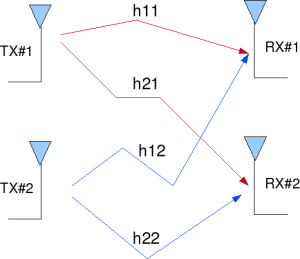
Figure: 2 Transmit 2 Receive (2×2) MIMO channel
Let us now try to understand the math for extracting the two symbols which interfered with each other. In the first time slot, the received signal on the first receive antenna is,
y1=h1,1x1+h1,2 x2+n1=[h1,1 h1,2][x1;x2] +n1
The received signal on the second receive antenna is,
y2=h2,1x1+h2,2x2+n2=[h2,1 h2,2][x1;x2]
y1,y2 are the received symbol on the first and second antenna respectively,where
h1,1 is the channel from 1st transmit antenna to 1st receive antenna,
h1,2 is the channel from 2nd transmit antenna to 1st receive antenna,
h2,1 is the channel from 1st transmit antenna to 2nd receive antenna,
h2,2 is the channel from 2nd transmit antenna to 2nd receive antenna,
x1,x2 are the transmitted symbols and
n1,n2 is the noise on 1st,2nd receive antennas.
We assume that the receiver knows h1,1, h1,2, h2,1and h2,2. The receiver also knows y1and y2. The unknown s are x1 and x2.
For convenience, the above equation can be represented in matrix notation as follows:
[y1;y2]=[h1,1 h1,2;h2,1 h2,2]+[n1;n2]
Equivalently,
y=Hx+n
No comments:
Post a Comment